World Wide CTF 2025 - Rhythmic Vault
Rhythmic Vault⌗
Challenge Description⌗
Brand new, fun and race-free verification for my flags. NOTE: Owning the game is not neccesary nor helpful in solving the task. Everything you need is oficially downloadable for free!
Challenge Author: Maximxls
Points: 500
Category: Reverse Engineering
Solves: 3
Overview⌗
We are given a Rhythm Doctor level file.
Rhythm Doctor is a rhythm game where you heal patients by defibrillating in time to their heartbeats.
It can be opened with the official (and free) level editor.
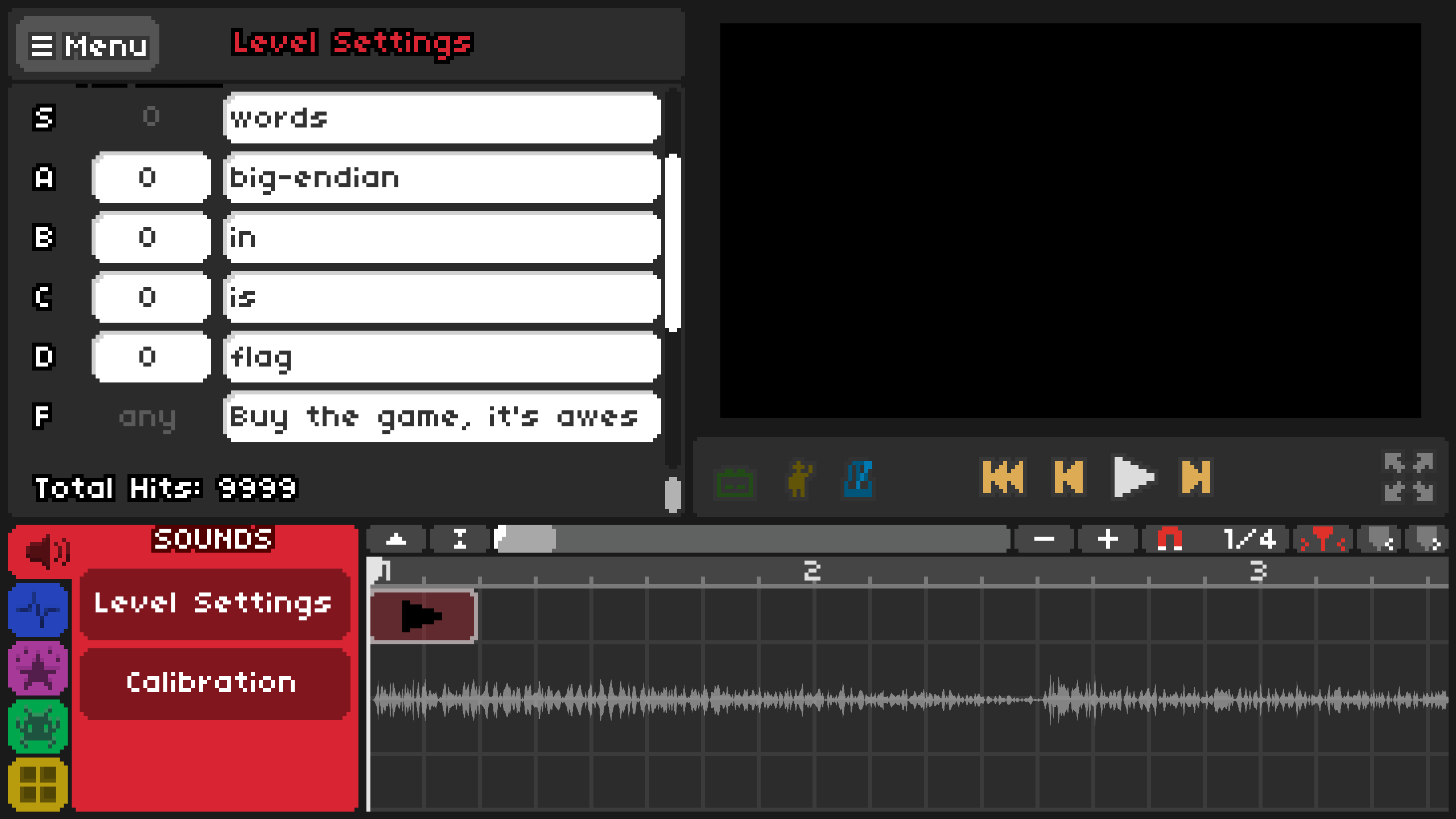
On navigating to the level settings in the editor we get our first clue- flag is in big-endian words. We can also run the game through the editor and seemed to go through 16 “rounds” and then displayed Incorrect.
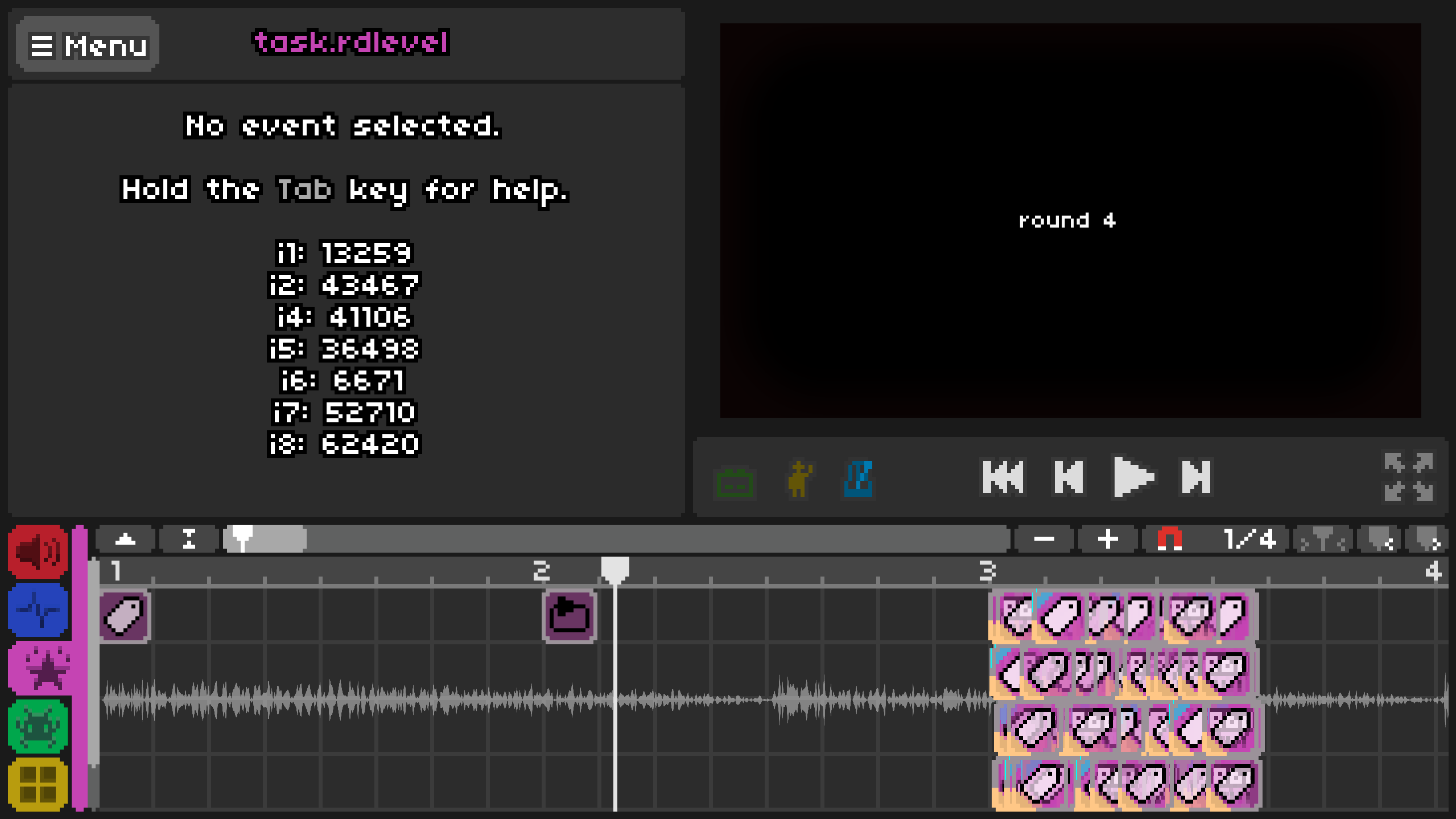
The actions tab displayed hundreds of tag-like blocks in the bottom section and had variables from i1 to i8 displayed with the changing values. None of this made any sense so first I had to figure out what all of this meant.
How Rhythm Doctor’s Level Editor Works⌗
I’ll only be going through the small section of the editor that matters for this challenge (specifically tags, variables and conditionals) but these are good resources if you want to explore it further:
RDCode is using Call Custom Method Event or Custom Conditional Events to essentially write a program in Rhythm Doctor to do various things.
Variables - Rhythm Doctor contains a bunch of editable variables that can be modified and used in rdcode:
- 10 integer variables (i0-i9)
- 10 float variables (f0-f9)
- 10 boolean variables (b0-b9)
- buttonPressCount(also an integer)
These variables can be used in call custom methods, conditionals and floating texts along with basic arithmetic and logical operators.
In this challenge we mostly care about i0-i9 and f0-f9 and only integer values were stored in the float variables.
Conditionals - Self explanatory, they check for conditions to trigger certain actions.
Tags - They allow a group of events to be executed together(kinda like functions). They can be disabled, which prevents them from running.
So by combining all these components actual programs can be created that control the behaviour of the level which is what seems to be going on in this challenge.
Parsing RDCode⌗
It was not clear what each of the tags were doing through the level editor and how they flowed between each other. I realised that a .rdlevel file is essentially a really big json file with all the tags and conditionals, so I could parse it directly to gain more information on it’s working.
A standard tag in the level file would be something like this:
{"bar": 3, "beat": 1.399738394220206, "y": 3, "tag": "15", "type": "TagAction", "Action": "Run", "Tag": "16"}
It has it’s beat location, and also what the action of the tag is - in this case this was tag 15 and it’s action was running tag 16. There are various actions like running, enabling or disabling another tag or running a custom method.
{"bar": 3, "beat": 4.797844782833935, "y": 0, "tag": "19", "type": "CallCustomMethod", "methodName": "i9 = i8", "executionTime": "OnBar", "sortOffset": 0}
This tag for example set i9 to the value of i8.
The file also had all it’s conditionals at the end like this one:
{"type": "Custom", "tag": "", "name": "", "id": 42, "expression": "i0 != 0"}
The id of a conditional is important since a tag calls a conditional in the format idd0, for example the above conditional with id 42 is called in the tag below with "if": "42d0":
{"bar": 3, "beat": 2.834561844092942, "y": 1, "tag": "142", "type": "CallCustomMethod", "if": "42d0", "methodName": "activeDialogues = 1", "executionTime": "OnBar", "sortOffset": 0}
With all this information I asked Claude to make a script to parse every tag and conditional and give me a cleaner overview of the rdcode along with the flow of commands. The parsed rdcode is in parsed_level.txt.
Analysis of the Level’s RDCode⌗
So the execution of the program start’s from the main tag and each tag might run some instructions and calls another tag(either if some conditons are met or directly). If it ever calls a tag that does not exist, you can consider it to be a break statement and it returns to the outer block(or in this case the tag that called this block of tags).
Essentially this is the flow of the program:
main tag
initialize i4-i9 and f0-f9 with fake flag values
initialize i1<-42591 and i2<-i2 = i1 * 27342 % 65537
start the round loop(runs for 16 rounds)
start round
run the affine_prepare tag
for each variable x from i4 to i9 and f0 to f9:
x = (i1*x + i2)%65537
run affine_prepare tag
end loop
shift variables(f9<-f8, f8<-f7....f0<-i9....i4<-f9)
end loop
checks each of the variables from i4-i9 and f0-f9 with constant values
if all checks pass - display Correct Flag!
else - display Incorrect
The affine_prepare tag does the following:
i3 = i1
i2 * 31149 % 65537
i2 = i3 * 17627 % 65537
if i1 > 32766 -> i1 = i1/3
Each of the flag variable(i4-i9 and f0-f9) contains two bytes of the flag converted to integers(this is where the initial clue comes in to play). The flag currently stored comes out to be wwf{fakefakefakefakefakefakefak}.
Now with this our goal finally becomes clear, we need to find what the flag variables need to be initialized with such that it passes all the final checks.
Solving the Challenge⌗
First we need to simulate what is happening in RDCode in python. This should have been an easy task, but it took a lot of my time and painstaking debugging. The reason for this is because RDCode’s / operator automatically rounds the number unlike python’s // and because we are dealing with modular math, even a difference of one vastly changes the final output. This was fixed by using int(round(a/b)) instead.
Simulation Script:
# Initial setup
i1 = 42591
i2 = i1 * 27342 % 65537
i3 = 1
i_vars = [0] * 10 # i0 to i9, used only indices 4-9
f_vars = [0] * 10 # f0 to f9
# initial fake flag values
i_vars[4:10] = [30583, 26235, 26209, 27493, 26209, 27493]
f_vars[0:10] = [26209, 27493, 26209, 27493, 26209, 27493, 26209, 27493, 26209, 27517]
# Initial affine prepare
i3 = i1
i1 = (i2 * 31149) % 65537
i2 = (i3 * 17627) % 65537
if i1 > 32766:
i1 = int(round(i1 / 3))
# 16 rounds simulation
for round_num in range(16):
for j in range(4, 10):
i3 = i1 * i_vars[j] + i2
i_vars[j] = i3 % 65537
# affine prepare
i3 = i1
i1 = (i2 * 31149) % 65537
i2 = (i3 * 17627) % 65537
if i1 > 32766:
i1 = int(round(i1 / 3))
i3 = 0
for j in range(10):
i3 = i1 * f_vars[j] + i2
f_vars[j] = i3 % 65537
# affine prepare
i3 = i1
i1 = i2 * 31149 % 65537
i2 = i3 * 17627 % 65537
if i1 > 32766:
i1 = int(round(i1 / 3))
# Shift operation
i3 = f_vars[9]
all_vars = f_vars + i_vars[4:10]
all_vars = [all_vars[-1]] + all_vars[:-1]
f_vars = all_vars[:10]
i_vars[4:10] = all_vars[10:]
i3 = 0
print(f"Round {round_num + 1}:")
print(*f_vars, *i_vars[4:10])
After making a valid simulation that matched the level’s rdcode, I found an important observation.
So the final constraints for each of the variables are:
i4==33601 i5==10760 i6==62873 i7==63911 i8==39745 i9==62471 f0==65158 f1==29652 f2==39777 f3==12164 f4==20416 f5==33945 f6==18465 f7==17245 f8==13049 f9==40799
But even with the fake flag values, the simulation was getting the same final i4 and i5 values as the contraints. This was because each variable represented two characters, so i4 and i5 represented the flag wrapper ww and f{ which was the same for both the fake flag and the actual flag.
The reason this is important is because it meant that the final output of one variable is independent of the initial values in the other variables and it only depends on two factors: initial value in that variable and index of the variable(consider i4 to be index 0 and f9 to be index 15).
In each round the values in the variables are shifted to the variable on the left, but since there are 16 variables in total and 16 rounds, by the end of all the rounds it comes back to the initial variable.
We know that the max initial value in each variable is 65537 due to the modulus used in calculation, so we can brute the initial value in each variable separately until it matches the constraint. Once we find all the initial values for each of the flag variables, we can convert each of them to bytes and get the flag!
Final Solve Script⌗
def brute(idx, val):
for x in range(65537):
i1 = 42591
i2 = i1 * 27342 % 65537
i3 = 1
i_vars = [0] * 10
f_vars = [0] * 10
if idx < 6:
i_vars[idx+4] = x
else:
f_vars[idx-6] = x
i3 = i1
i1 = (i2 * 31149) % 65537
i2 = (i3 * 17627) % 65537
if i1 > 32766:
i1 = int(round(i1 / 3))
for _ in range(16):
for j in range(4, 10):
i3 = i1 * i_vars[j] + i2
i_vars[j] = i3 % 65537
i3 = i1
i1 = (i2 * 31149) % 65537
i2 = (i3 * 17627) % 65537
if i1 > 32766:
i1 = int(round(i1 / 3))
i3 = 0
for j in range(10):
i3 = i1 * f_vars[j] + i2
f_vars[j] = i3 % 65537
i3 = i1
i1 = i2 * 31149 % 65537
i2 = i3 * 17627 % 65537
if i1 > 32766:
i1 = int(round(i1 / 3))
i3 = f_vars[9]
temp = f_vars[9]
f_vars[9:0:-1] = f_vars[8::-1]
f_vars[0] = i_vars[9]
i_vars[9:4:-1] = i_vars[8:3:-1]
i_vars[4] = temp
i3 = 0
if idx < 6:
if i_vars[idx+4] == val:
return x
else:
if f_vars[idx-6] == val:
return x
return None
constraints = [33601,10760,62873,63911,39745,62471,65158,29652,39777,12164,20416,33945,18465,17245,13049,40799]
flag = b''
for i in range(16):
flag += brute(i,constraints[i]).to_bytes(2,'big')
print(flag)
Flag⌗
wwf{I4n_1s_s0_pr0ud_0f_y0u_648f}